Symétrie Axiale
Symétrie Axiale
Partie 1 : Première Approche de la Symétrie Axiale : un Pliage
La première transformation que nous aborderons est la symétrie axiale.
Dans l’animation ci-dessous, on pourra regarder l’effet de cette symétrie axiale sur la figure de départ, le poisson.
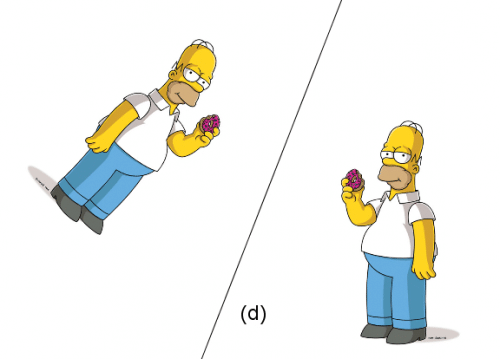
La première transformation que nous aborderons est la symétrie axiale.
Dans l’animation ci-dessous, on pourra regarder l’effet de cette symétrie axiale sur la figure de départ, le poisson.
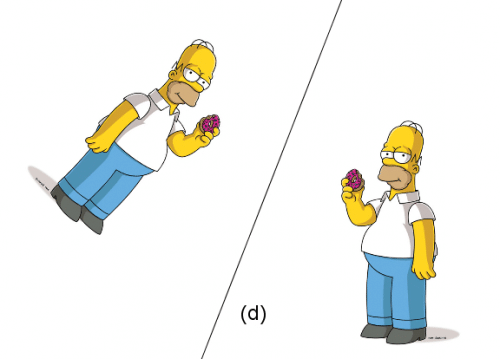
Regarder l'Animation d'Introduction
Regarder l'Animation d'Introduction
Regardons maintenant l’effet de la symétrie dans des situations réelles :
Regardons maintenant l’effet de la symétrie dans des situations réelles :
Regarder les Exemples d'Effets Miroirs
Regarder les Exemples d'Effets Miroirs
Partie 2 : Symétrie Axiale et Médiatrice
Regardons pour cela les résultats de symétries effectuées sur des figures géométriques simples.
Regarder l'Animation : Exemples de Figures et leur Symétrique
Regarder l'Animation : Exemples de Figures et leur Symétrique
On en vient même à mieux cerner ce qui se passe lorsque l’on a qu’un seul pointM au départ :
- l’axe de symétrie est perpendiculaire au segment [MM’]
- cet axe passe également par le milieu du segment.
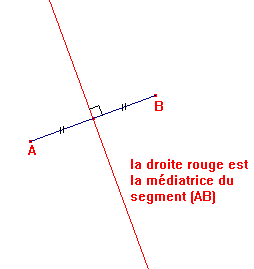
On appelle cette droite une médiatrice. En voici la définition :
Définition : La médiatrice d’un segment est la droite qui coupe ce segment perpendiculairement et en son milieu.
On en vient même à mieux cerner ce qui se passe lorsque l’on a qu’un seul pointM au départ :
- l’axe de symétrie est perpendiculaire au segment [MM’]
- cet axe passe également par le milieu du segment.
On appelle cette droite une médiatrice. En voici la définition :
Définition : La médiatrice d’un segment est la droite qui coupe ce segment perpendiculairement et en son milieu.

Partie 3 : Propriétés des Médiatrices
Il faudra retenir surtout ces 2 là :
Propriété 1 : Si un point est situé sur la médiatrice d’un segment, alors il est situé à la même distance des extrémités de ce segment.
Et la propriété réciproque :
Propriété 2 : Si un point est situé à la même distance des extrémités d’un segment, alors il se trouve sur la médiatrice de ce segment.
Regarder l'Animation : Propriétés de la Médiatrice
Regarder l'Animation : Propriétés de la Médiatrice
Partie 4 : Comment Tracer le Symétrique d’une Figure
Dans l’animation suivante, on pourra regarder une manière de tracer ce symétrique : On va faire en sorte que l’axe de symétrie devienne la médiatrice de tous les segments dont les 2 extrémités sont un point et son image.
Pour cela, pour un point M dont on veut le symétrique :
- On tracera une demi-droite d’origine M et qui est perpendiculaire à l’axe de symétrie.
- On placera l’image M’ de sorte que l’axe de symétrie passe au milieu du segment [MM’]
Regarder l'Animation : Méthode de Tracé d'un Symétrique
Regarder l'Animation : Méthode de Tracé d'un Symétrique
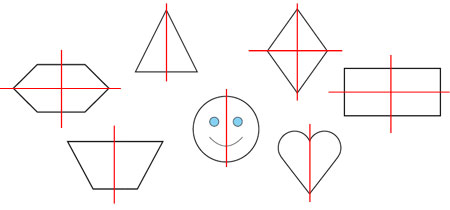
Partie 5 : Axes de Symétrie d’une figure
En voici quelques exemples ci-contre.